|
| 1 | + |
| 2 | +<p align="center"> |
| 3 | + <a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a> |
| 4 | + <a href="https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw"><img src="https://img.shields.io/badge/刷题-微信群-green" alt=""></a> |
| 5 | + <a href="https://img-blog.csdnimg.cn/20201210231711160.png"><img src="https://img.shields.io/badge/公众号-代码随想录-brightgreen" alt=""></a> |
| 6 | + <a href="https://space.bilibili.com/525438321"><img src="https://img.shields.io/badge/B站-代码随想录-orange" alt=""></a> |
| 7 | +</p> |
| 8 | + |
| 9 | +## 39. 组合总和 |
| 10 | + |
| 11 | +题目链接:https://leetcode-cn.com/problems/combination-sum/ |
| 12 | + |
| 13 | +给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 |
| 14 | + |
| 15 | +candidates 中的数字可以无限制重复被选取。 |
| 16 | + |
| 17 | +说明: |
| 18 | + |
| 19 | +* 所有数字(包括 target)都是正整数。 |
| 20 | +* 解集不能包含重复的组合。 |
| 21 | + |
| 22 | +示例 1: |
| 23 | +输入:candidates = [2,3,6,7], target = 7, |
| 24 | +所求解集为: |
| 25 | +[ |
| 26 | + [7], |
| 27 | + [2,2,3] |
| 28 | +] |
| 29 | + |
| 30 | +示例 2: |
| 31 | +输入:candidates = [2,3,5], target = 8, |
| 32 | +所求解集为: |
| 33 | +[ |
| 34 | + [2,2,2,2], |
| 35 | + [2,3,3], |
| 36 | + [3,5] |
| 37 | +] |
| 38 | + |
| 39 | +## 思路 |
| 40 | + |
| 41 | +[B站视频讲解-组合总和](https://www.bilibili.com/video/BV1KT4y1M7HJ) |
| 42 | + |
| 43 | + |
| 44 | +题目中的**无限制重复被选取,吓得我赶紧想想 出现0 可咋办**,然后看到下面提示:1 <= candidates[i] <= 200,我就放心了。 |
| 45 | + |
| 46 | +本题和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)和区别是:本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。 |
| 47 | + |
| 48 | +本题搜索的过程抽象成树形结构如下: |
| 49 | + |
| 50 | + |
| 51 | +注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回! |
| 52 | + |
| 53 | +而在[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w) 中都可以知道要递归K层,因为要取k个元素的组合。 |
| 54 | + |
| 55 | +## 回溯三部曲 |
| 56 | + |
| 57 | +* 递归函数参数 |
| 58 | + |
| 59 | +这里依然是定义两个全局变量,二维数组result存放结果集,数组path存放符合条件的结果。(这两个变量可以作为函数参数传入) |
| 60 | + |
| 61 | +首先是题目中给出的参数,集合candidates, 和目标值target。 |
| 62 | + |
| 63 | +此外我还定义了int型的sum变量来统计单一结果path里的总和,其实这个sum也可以不用,用target做相应的减法就可以了,最后如何target==0就说明找到符合的结果了,但为了代码逻辑清晰,我依然用了sum。 |
| 64 | + |
| 65 | +**本题还需要startIndex来控制for循环的起始位置,对于组合问题,什么时候需要startIndex呢?** |
| 66 | + |
| 67 | +我举过例子,如果是一个集合来求组合的话,就需要startIndex,例如:[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)。 |
| 68 | + |
| 69 | +如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:[回溯算法:电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A) |
| 70 | + |
| 71 | +**注意以上我只是说求组合的情况,如果是排列问题,又是另一套分析的套路,后面我再讲解排列的时候就重点介绍**。 |
| 72 | + |
| 73 | +代码如下: |
| 74 | + |
| 75 | +```C++ |
| 76 | +vector<vector<int>> result; |
| 77 | +vector<int> path; |
| 78 | +void backtracking(vector<int>& candidates, int target, int sum, int startIndex) |
| 79 | +``` |
| 80 | +
|
| 81 | +* 递归终止条件 |
| 82 | +
|
| 83 | +在如下树形结构中: |
| 84 | +
|
| 85 | + |
| 86 | +
|
| 87 | +从叶子节点可以清晰看到,终止只有两种情况,sum大于target和sum等于target。 |
| 88 | +
|
| 89 | +sum等于target的时候,需要收集结果,代码如下: |
| 90 | +
|
| 91 | +```C++ |
| 92 | +if (sum > target) { |
| 93 | + return; |
| 94 | +} |
| 95 | +if (sum == target) { |
| 96 | + result.push_back(path); |
| 97 | + return; |
| 98 | +} |
| 99 | +``` |
| 100 | + |
| 101 | +* 单层搜索的逻辑 |
| 102 | + |
| 103 | +单层for循环依然是从startIndex开始,搜索candidates集合。 |
| 104 | + |
| 105 | +**注意本题和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)的一个区别是:本题元素为可重复选取的**。 |
| 106 | + |
| 107 | +如何重复选取呢,看代码,注释部分: |
| 108 | + |
| 109 | +```C++ |
| 110 | +for (int i = startIndex; i < candidates.size(); i++) { |
| 111 | + sum += candidates[i]; |
| 112 | + path.push_back(candidates[i]); |
| 113 | + backtracking(candidates, target, sum, i); // 关键点:不用i+1了,表示可以重复读取当前的数 |
| 114 | + sum -= candidates[i]; // 回溯 |
| 115 | + path.pop_back(); // 回溯 |
| 116 | +} |
| 117 | +``` |
| 118 | + |
| 119 | +按照[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中给出的模板,不难写出如下C++完整代码: |
| 120 | + |
| 121 | +```C++ |
| 122 | +// 版本一 |
| 123 | +class Solution { |
| 124 | +private: |
| 125 | + vector<vector<int>> result; |
| 126 | + vector<int> path; |
| 127 | + void backtracking(vector<int>& candidates, int target, int sum, int startIndex) { |
| 128 | + if (sum > target) { |
| 129 | + return; |
| 130 | + } |
| 131 | + if (sum == target) { |
| 132 | + result.push_back(path); |
| 133 | + return; |
| 134 | + } |
| 135 | + |
| 136 | + for (int i = startIndex; i < candidates.size(); i++) { |
| 137 | + sum += candidates[i]; |
| 138 | + path.push_back(candidates[i]); |
| 139 | + backtracking(candidates, target, sum, i); // 不用i+1了,表示可以重复读取当前的数 |
| 140 | + sum -= candidates[i]; |
| 141 | + path.pop_back(); |
| 142 | + } |
| 143 | + } |
| 144 | +public: |
| 145 | + vector<vector<int>> combinationSum(vector<int>& candidates, int target) { |
| 146 | + result.clear(); |
| 147 | + path.clear(); |
| 148 | + backtracking(candidates, target, 0, 0); |
| 149 | + return result; |
| 150 | + } |
| 151 | +}; |
| 152 | +``` |
| 153 | +
|
| 154 | +## 剪枝优化 |
| 155 | +
|
| 156 | +在这个树形结构中: |
| 157 | +
|
| 158 | + |
| 159 | +
|
| 160 | +以及上面的版本一的代码大家可以看到,对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。 |
| 161 | +
|
| 162 | +其实如果已经知道下一层的sum会大于target,就没有必要进入下一层递归了。 |
| 163 | +
|
| 164 | +那么可以在for循环的搜索范围上做做文章了。 |
| 165 | +
|
| 166 | +**对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历**。 |
| 167 | +
|
| 168 | +如图: |
| 169 | +
|
| 170 | +
|
| 171 | +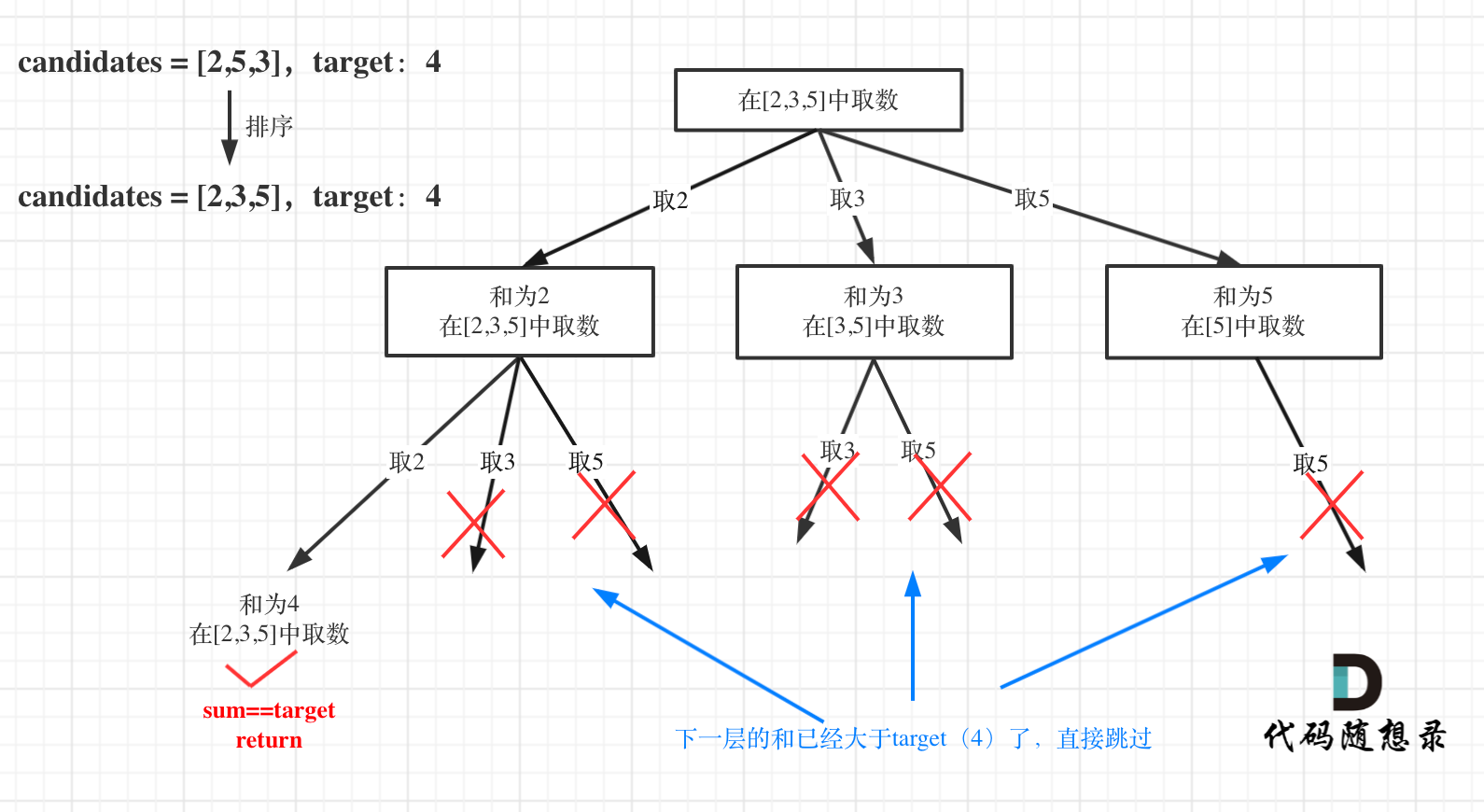 |
| 172 | +
|
| 173 | +for循环剪枝代码如下: |
| 174 | +
|
| 175 | +``` |
| 176 | +for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) |
| 177 | +``` |
| 178 | +
|
| 179 | +整体代码如下:(注意注释的部分) |
| 180 | +
|
| 181 | +```C++ |
| 182 | +class Solution { |
| 183 | +private: |
| 184 | + vector<vector<int>> result; |
| 185 | + vector<int> path; |
| 186 | + void backtracking(vector<int>& candidates, int target, int sum, int startIndex) { |
| 187 | + if (sum == target) { |
| 188 | + result.push_back(path); |
| 189 | + return; |
| 190 | + } |
| 191 | +
|
| 192 | + // 如果 sum + candidates[i] > target 就终止遍历 |
| 193 | + for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) { |
| 194 | + sum += candidates[i]; |
| 195 | + path.push_back(candidates[i]); |
| 196 | + backtracking(candidates, target, sum, i); |
| 197 | + sum -= candidates[i]; |
| 198 | + path.pop_back(); |
| 199 | +
|
| 200 | + } |
| 201 | + } |
| 202 | +public: |
| 203 | + vector<vector<int>> combinationSum(vector<int>& candidates, int target) { |
| 204 | + result.clear(); |
| 205 | + path.clear(); |
| 206 | + sort(candidates.begin(), candidates.end()); // 需要排序 |
| 207 | + backtracking(candidates, target, 0, 0); |
| 208 | + return result; |
| 209 | + } |
| 210 | +}; |
| 211 | +``` |
| 212 | + |
| 213 | +## 总结 |
| 214 | + |
| 215 | +本题和我们之前讲过的[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)有两点不同: |
| 216 | + |
| 217 | +* 组合没有数量要求 |
| 218 | +* 元素可无限重复选取 |
| 219 | + |
| 220 | +针对这两个问题,我都做了详细的分析。 |
| 221 | + |
| 222 | +并且给出了对于组合问题,什么时候用startIndex,什么时候不用,并用[回溯算法:电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A)做了对比。 |
| 223 | + |
| 224 | +最后还给出了本题的剪枝优化,这个优化如果是初学者的话并不容易想到。 |
| 225 | + |
| 226 | +**在求和问题中,排序之后加剪枝是常见的套路!** |
| 227 | + |
| 228 | +可以看出我写的文章都会大量引用之前的文章,就是要不断作对比,分析其差异,然后给出代码解决的方法,这样才能彻底理解题目的本质与难点。 |
| 229 | + |
| 230 | +------------------------ |
| 231 | + |
| 232 | +* 微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw) |
| 233 | +* B站:[代码随想录](https://space.bilibili.com/525438321) |
| 234 | +* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ) |
| 235 | + |
| 236 | + |
0 commit comments