LeetCode 中有许多与字符串、数组、链表相关的题目,都用到了一种称为双指针two pointer的方法,顾名思义,双指针是指有两个游标指针指向不同的位置,注意此处的指针与C/C++语言中的指针并不完全相同,可以理解为指向不同位置的两个游标。
双指针有两种类型,一种是“头尾双指针”,一种是“快慢双指针”。双指针是针对特定问题而提出的一种算法思想。
问题描述:
给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。
说明:
返回的下标值(index1 和 index2)不是从零开始的。 你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。 示例:
输入: numbers = [2, 7, 11, 15], target = 9 输出: [1,2] 解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
方法一:暴力破解法 遍历所有两个不同的数之和,查看和是否与目标数相同,如果相同,返回两个加数和坐标。如果不存在这样的两个数之和与目标数相等,则证明不存在解。
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
for i in range (0, len(numbers), 1):
for j in range (i + 1, len(numbers), 1):
if numbers[i] + numbers[j] == target:
return [i + 1, j + 1]
return []方法二:双指针法。利用数组是有序数组的特性,使用头尾双指针分别指向两个数组元素,如果两数之和比目标值大,则向左移动尾指针,反之,向右移动手指针。如果两指针相遇后,仍然未找到两数和等于目标值,即未找到解。
class Solution:
"""
" type namber: List[int]
" type target: int
" rtype: List[int]
"""
def twoSum(self, number:List[int], target: int)->List[int]:
left, right = 0, len(numbers) - 1
while left < right:
if (numbers[left] + numbers[right] == target):
return [left + 1, right + 1]
elif numbers[left] + numbers[right] < target:
left += 1
else:
right -= 1
return []给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明: 你不能倾斜容器,且 n 的值至少为 2
最大储水能力。
方法一:暴力法。遍历所有可能储水情况,找到其中的最大值即可。但该方法会计算超时。
class Solution {
public:
int maxArea (vector<int>& height) {
int res = 0;
int area = 0;
for (int i = 0; i < height.size() - 1; i++)
for (int j = i + 1; j < height.size(); j++) {
area = (j - i) * min(height[i], height[j]);
if (area > res)
res = area;
}
return res;
}
};复杂度分析:
- 时间复杂度:O(n^2)。对每一对儿进行计算,总计算结果一共 n(n - 1) / 2.
- 空间复杂度:O(1)。只需要额外的一个变量存放最大面积即可。
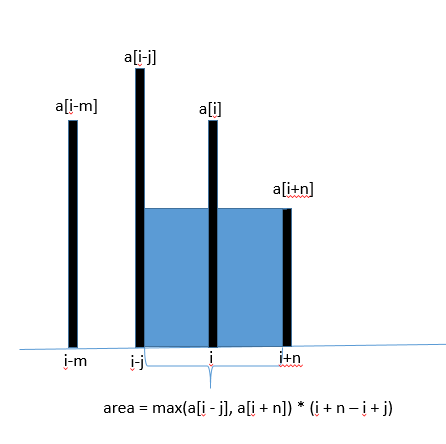
方法二:双指针法。如下图所示,任意两个数组元素(a[i + n] 和 a[i - j ])的最大储水能力为
area = max(a[i + n], a[i - j]) * (i + n - (i - j))
选取数组的开始和末尾元素作为首尾双指针的起始位置,计算两个指针可容纳的储水面积,之后移动数值较小的指针向中间靠拢,重新计算两个指针可容纳的储水面积并与之前的最大面积做比较,以此类推,直至两个指针相遇位置,即可得最大面积。
下面给出这种计算步骤和合理性说明。
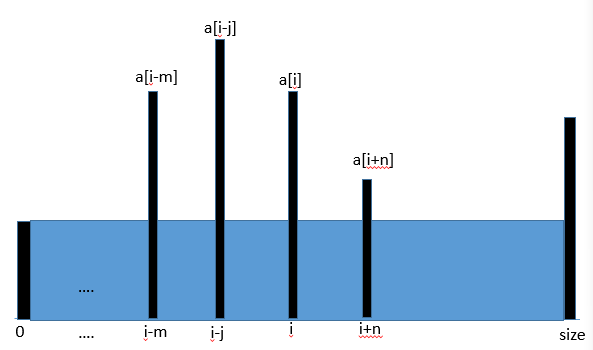
- 选取第一个和最后一个元素时,假设a[0]是较小者,两元素的最大储水能力为
area = max(a[0], a[size]) * (size) = a[0] * size.则a[0]与其他任一元素的储水能力不可能超过 area,因为max(a[0], a[i]) <= a[0],而i < size,所以max(a[0], a[i]) * i < max(a[0], a[size]) * (size). - 移动左指针指向元素a[1],计算面积的大小,并与1中计算的面积作比较,取较大者。按照同样的原则,移动a[1]和a[size]中较小者,向中间靠拢。
- 重复步骤2.直至两指针指向同一元素,返回最大值。
class Solution:
def maxArea(self, height: List[int]) -> int:
#init the param
left, right, width, res = 0, len(height) - 1, len(height) - 1, 0
for w in range (width, 0, -1):
if height[left] < height[right]:
res, left = max(res, height[left] * w), left + 1
else:
res, right = max(res, height[right] * w), right - 1
return res复杂度分析:
- 时间复杂度:O(n)。遍历一次 vector 中的所有元素。
- 空间复杂度:O(1)。使用恒定空间。
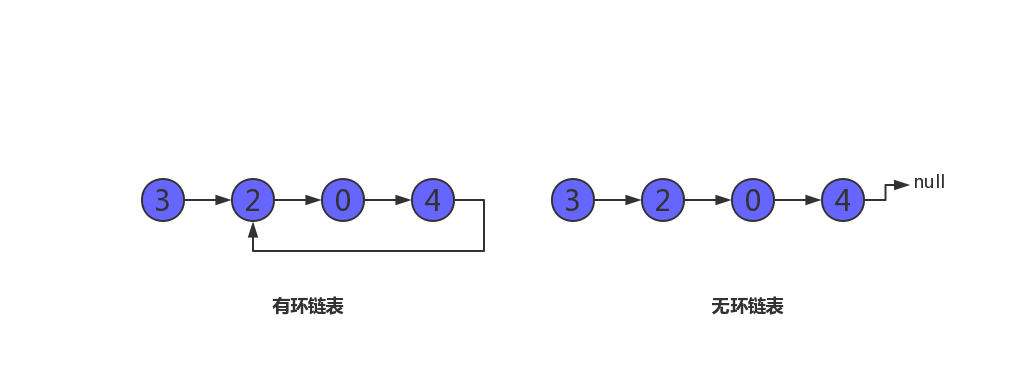
给定一个链表,判断链表中是否有环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
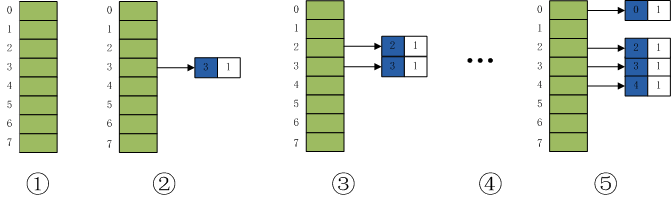
方法一:哈希法。遍历整个链表,查看是否存在某个节点遍历过两次,如果存在这样的节点,就证明有环存在,否则,没有环。因为要查看节点出现的次数,所以很容易想到使用 Hash Table 存储之前遍历过的节点。
如上图所示,首先创建一个空的哈希表,依次往哈希表中插入链表的节点 3-->2-->0-->4,如果链表有环,接下来再继续查看哈希表中是否有下一个节点 2,如果有此节点,则证明有环;否则,无环。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
# solution using set
class Solution:
def hasCycle(self, haed:ListNode)->bool:
# check the input param
if head is None:
return False
node_set = {}
while head.next:
node_set[head] = True
if head.next in node_set:
return True
head = head.next
return False复杂度分析:
- 时间复杂度:O(n)。遍历链表中的每个节点,添加节点到哈希表所用时间为O(1)。
- 空间复杂度: O(n)。所用空间取决于添加到哈希表中的节点个数,最多为 n。
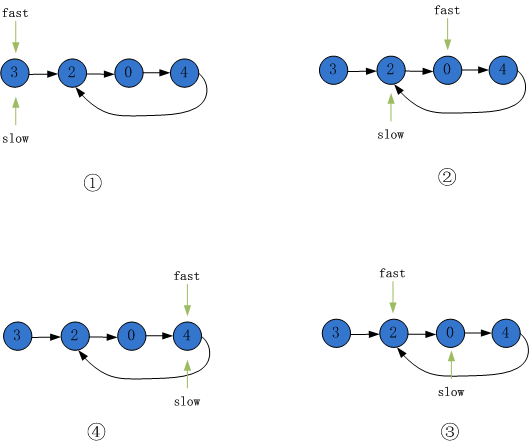
方法二:双指针法。类似于两个不同速度的人跑步,如果是围着操场跑圈,快的总能多跑一圈后追上慢的;如果是直线跑,除了起点外,两人就永远不会在相遇了。同样的道理,从链表的起始点开始给到两个快速、慢速指针,如果有环,快速指针总能追上慢速指针,如果没有环,快速指针提前到链表尾部,结束。
如上图所示,将快慢指针同时初始化为第一个节点,如图1所示。快指针每次移动步长为2,慢指针每次移动步长为1.慢指针到达节点2时,进入环内,此时快指针指向节点0.如图2所示。继续一定,快指针第二次指向2节点,慢指针指向0节点,如图3所示。最后,快指针慢指针在节点4处再次相遇,证明有环,如图4所示。如果无环,快指针会提前到达链表终点。
# solution using two pointer
class Solution:
def hasCycle(self, head:ListNode)->bool:
# check the input param
if head == None or head.next == None:
return False
pslow = pfast = head
while pfast != None and pfast.next != None:
pslow = pslow.next
pfast = pfast.next.next
if pfast == pslow:
break
if pfast == None or pfast.next == None:
return False
elif pfast == pslow:
return True
return False复杂度分析:
- 时间复杂度:O(n)。n 为链表中节点的个数。为分析时间复杂度,考虑两种情况:
- 链表无环: 快速指针到达链表终点,结束。执行时间与链表长度相关,即O(n).
- 链表有环:将慢速指针的整个路径分为两部分,环内部分和环外部分。① 当慢速指针在环外移动了 N 步以后,快速指针在环内移动了 N 步。② 此时快慢指针都在环内,假设环的长度为 K,环内快速指针追上慢指针,最糟糕的情况为 O(K),整个过程最糟糕情况为O(N + K),即 O(N)。
- 空间复杂度:O(1)。因为使用了两个节点,所以空间复杂度为O(1)。
给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
示例 1:
给定数组 nums = [1,1,2],
函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。
示例 2:
给定 nums = [0,0,1,1,1,2,2,3,3,4],
函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。 (待续...)
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
| 输入 | 输出 | 备注 |
|---|---|---|
| "abcabcbb" | 3 | substr:"abc", len is 3 |
| "bbbbb" | 1 | substr:"b", len is 1 |
| "pwwkew" | 3 | substr:"wke", len is 3 |
该问题主要包含两个子问题:1.从字符串中找到子字符串;2.针对子字符串,查看其中是否有重复的字符。下面的几种方法也是针对上面的两个子问题进行优化的。
方法一:暴力法。遍历所有子字符串,针对每个字符串,查看是否含有重复字符。时间超时。
class Solution1 {
private:
bool allUnique (string s) {
unordered_map<char, int> mapping;
for (int i = 0; i < s.size(); i++) {
if (mapping.find(s[i]) == mapping.end())
mapping.insert({s[i], 1});
else
return false;
}
return true;
}
public:
int lengthOfLongestSubstring (string s) {
int res = 0;
for (int i = 0; i < s.size(); i++)
for (int j = i; j < s.size(); j++)
if (allUnique(s.substr(i, j - i + 1)))
res = max(res, j - i + 1);
else
break;
return res;
}
};复杂度分析:
时间复杂度:O(n^3)。
统计子字符串时,两个循环所用时间为O(n^2),针对每个子字符串,查看是否有重复字符,所用时间为O(j - i),所以总时间复杂度为O(n^3)。
空间复杂度:O(min(n, m),其中n是字符串的长度,m是字符集的大小。
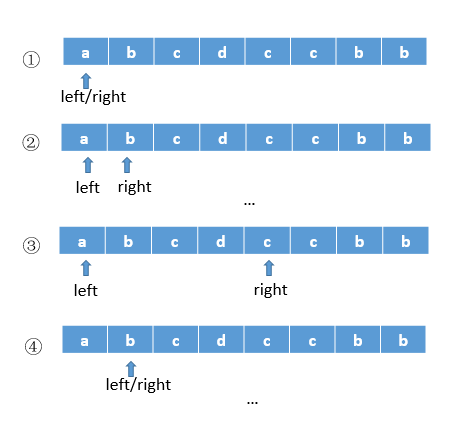
方法二:双指针法。该方法是对上面暴力法的优化。主要有两点优化。
- 针对子字符串是否含有重复字符的优化。替代上面的 allUnique 函数,使用了unordered_set 容器,来对子字符串进行了处理,使得时间复杂度降低到了O(n^2)。
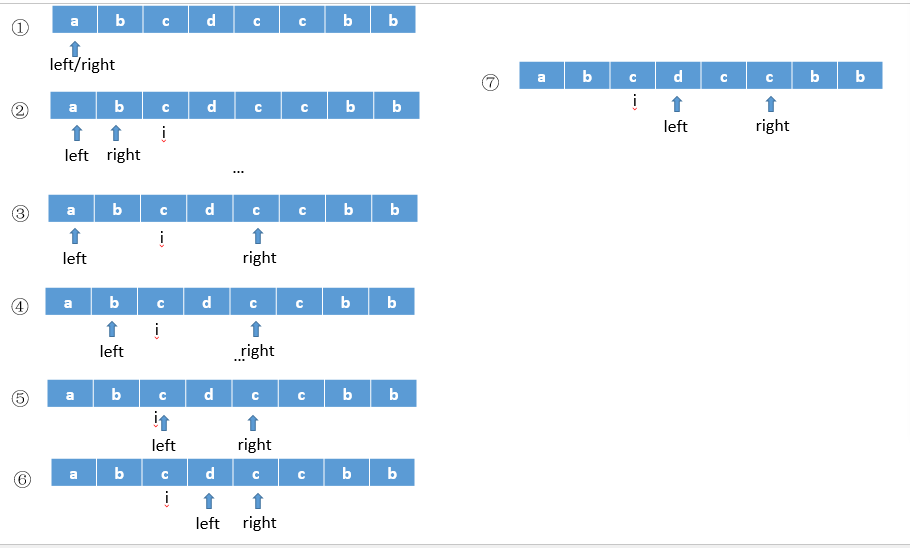
- 针对子字符串选择的优化。固定 left 的情况,只要找到 [left, right) 存在与 right 指针重复的字符,就跳出子循环,因为此时[left, right + i]一定含有重复字符。继续查看 left + 1 为起始的子字符串情况。如下图所示,当right 指向第二个 c 时,right 继续增加,子字符串一定包含重复字符 c。因此可以跳出子循环。该优化方案相对于方法一,少了步骤 4/5 两步。
//using two point && unordered_set
//used time:628ms
class Solution
def lengthOfLongestSubstring (self, s:str) -> int:
res, left, right = 0, 0, 0
settings = set()
for left in range(0, len(s), 1):
right = left
while (right < len(s)):
if (s[right] in settings):
break
else:
settings.add(s[right])
res = max(res, right - left + 1)
right = right + 1
settings.clear()
return res复杂度分析:
时间复杂度:O(n^2)。
空间复杂度:O(min(n, m),其中n是字符串的长度,m是字符集的大小。
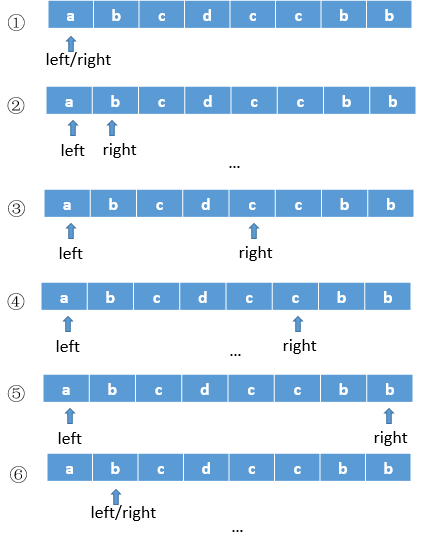
方法三:滑动窗口法。上面提到的两种方法本质上都是遍历所包含的子字符串。本方法继续对字符串的选择进行筛选。如下图所示,当 right 指针指向的字符,与 [left,right) 之间的 i 字符相同时,此时,只需要找到重复字符的位置 i,从该字符处往后查找即可;因为[left, i)的任一字符作为起始字符,与后面组合成无重复字符的字符串长度一定小于[left, right)。
//using two pointer && sliding window && unordered_set
//used time:28ms
class Solution
def lengthOfLongestSubstring (self, s:str) -> int:
res, left, right = 0, 0, 0
settings = set()
while right < len(s):
if s[right] in settings:
while left < right:
if s[left] == s[right]:
settings.discard(s[left])
left = left + 1
break
else:
settings.discard(s[left])
left = left + 1
settings.add(s[right])
res = max(res, right - left + 1)
right = right + 1
return res复杂度分析:
时间复杂度:O(2n), 即 O(n)。
空间复杂度:O(min(n, m),其中 n 是字符串的长度,m 是字符集的大小。
方法四:滑动窗口法。该方法是对方法三进一步优化。
- 首先,上面最left的移动是逐个移动,最后移动到 i + 1 位置的,本方法使用 unordered_map ,一次移动到 i + 1 的位置。该优化,相对于方法三,省去了步骤 4/5 两步。
- 其次,对退出条件作了进一步的优化,使用 right < s.size 的同时,添加了 left + res < s.size() 的限制,从而避免了一些无效子字符串的检查。
//using sliding window && two_pointer && unordered_map
//used time:8ms
class Solution:
def lengthOfLongestSubstring (self, s:str) -> int:
res, left, right = 0, 0, 0
dic = {}
while right < len(s) and left + res < len(s):
if s[right] in dic:
left = max(left, dic[s[right]] + 1)
dic[s[right]] = right
res = max(res, right - left + 1)
right = right + 1
return res复杂度分析:
时间复杂度:O(n)。
空间复杂度: O(min(m, n))。
对于可以使用双指针的问题,多多考虑使用的指针类型,是从一边开始的快慢指针,还是从两边开始的首尾指针。针对快慢指针,用于 sliding window 问题时,还可以考虑通过指针控制窗口的大小来优化算法。